7261. Трудный путь
Вася хорошо
выпил и теперь, когда он добрался до своей улицы, он полностью потерял чувство
направления. Поскольку он не помнит, с какой стороны его дом, он выбирает
направление наобум. Более того, на каждом перекрёстке он с вероятностью 50%
продолжает идти вперёд, а иначе разворачивается и идёт назад. Он настолько
потерял связь с реальностью, что может даже пройти мимо своего дома и не
заметить этого!
Пройдя n кварталов, Вася засыпает прямо на
улице. Проснувшись, он задаётся вопросом: какой у него был шанс заснуть рядом с
домом? Ведь от перекрёстка, от которого он начал свой путь, до перекрёстка
рядом с домом Васи всего m кварталов.
Помогите ему.
Вход. В одной строке содержатся два целых
числа n и m (1 ≤ n, m ≤ 1000).
Выход. Выведите
одно число – вероятность Васи заснуть на перекрёстке рядом со своим домом.
Выведите ответ с абсолютной погрешностью не более 10-7.
|
Пример входа 1 |
Пример выхода 1 |
|
1 1 |
0.5 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
1000
100 |
0.000169397 |
РЕШЕНИЕ
вероятность
Анализ алгоритма
Объявим
двумерный массив d, в котором d[time][x] равно вероятности оказаться в точке с
абсциссой x в момент времени time. Пусть изначально (в момент времени
t = 0) Вася находится в точке с
абсциссой x = n. Тогда d[0][n] = 1.
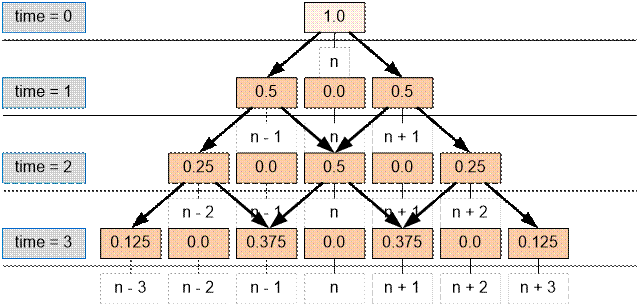
Вычислим d[i][j]
– вероятность того что Вася в момент времени i будет находиться в позиции j.
Для этого Васе следует находиться в момент времени i – 1 либо в позиции j –
1, либо в позиции j + 1. Тогда в
момент времени i он сможет попасть из
них в позицию j с вероятностью 50%.
То есть
d[i][j]
= (d[i – 1][j – 1] + d[i – 1][j + 1]) / 2
Рассмотрим
математическое решение задачи. Закодируем путь Васи последовательностью из 0 и
1. Пусть 1 соответствует движению вправо, а 0 влево. Пусть из n шагов,
которые совершил Вася, k шагов он сделал вправо. Тогда n – k шагов он сделал влево.
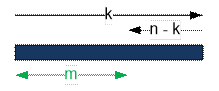
Нас интересует
вероятность того, что Вася переместился в одну из сторон (например вправо) на m кварталов.
Тогда должно выполняться: m + n – k
= k, откуда k = (m + n) / 2. Количество
последовательностей длины n с k единицами равно
. Поскольку Вася совершил n
перемещений, то у него имеется 2n
вариантов выбора различных путей. Следовательно вероятность того что Вася
пройдет вправо m кварталов, равна / 2n, где k = (m + n)
/ 2. Отметим, что искомая вероятность равна 0, если m + n нечетно. В этом случае Вася просто не сможет
попасть домой (m + n = 2k, то есть
четно).
Пример
Пусть Вася
совершит n = 3 шага.
Если m = 1, то k = (3 + 1) / 2 = 2 и
вероятность равна 
/ 23 = 3 / 8 = 0.375.
Если m = 3, то k = (3 + 3) / 2 = 3 и вероятность
равна 
/ 23 = 1 / 8 = 0.125.
Пусть Вася
совершит n = 4 шага.
Если m = 0, то k = (4 + 0) / 2 = 2 и вероятность
равна 
/ 24 = 6 / 16 = 0.375.
Если m = 2, то k = (4 + 2) / 2 = 3 и вероятность
равна 
/ 24 = 4 / 16 = 0.25.
Если m = 4, то k = (4 + 4) / 2 = 4 и вероятность
равна 
/ 24 = 1 / 16 = 0.0625.
Реализация алгоритма
Объявим
двумерный массив для вычисления вероятностей.
#define MAX 2010
double d[MAX][MAX];
Читаем входные данные. Инициализируем массив d.
scanf("%d %d",&n,&m);
memset(d,0,sizeof(d));
d[0][n]
= 1;
Пересчитываем вероятности согласно приведенного
рекуррентного соотношения.
for(i
= 1; i <= n; i++)
for(j = n -
i; j <= n + i; j++)
d[i][j] = (d[i-1][j-1] + d[i-1][j+1]) / 2;
Выводим ответ – вероятность того что Вася пройдет в одну
из сторон (например вправо) m
кварталов и найдет свой дом.
printf("%.9lf\n",d[n][n+m]);
Java реализация
import java.util.*;
public class Main
{
public static void main(String []args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
double d[][] = new double[n+1][2*n+1];
d[0][n] = 1;
for(int i = 1; i <= n; i++)
{
for(int j = n - i; j <= n + i; j++)
{
double a = (j - 1 < 0) ? 0 : d[i-1][j-1];
double b = (j + 1 > 2*n) ? 0 : d[i-1][j+1];
d[i][j] = (a + b) / 2;
// d[i][j] = (d[i-1][j-1] +
d[i-1][j+1]) / 2;
}
}
double res = (n + m > 2*n) ? 0 :
d[n][n+m];
System.out.println(res);
con.close();
}
}